Happy 115th birthday, spacetime!

Hermann Minkowski addressed the 80th Assembly of German Natural Scientists and Physicians #OTD in 1908, offering a radical four-dimensional reformulation of Einstein's theory of special relativity.

His opening lines:

The mathematician Paul Erdős had a fantasy that he'd die giving a lecture: he would prove a result, someone would ask about a generalization, he'd reply "I'll leave that to the next generation," and then he'd die.

He passed away at a conference in Warsaw #OTD in 1996, just after proving a new result.

I'm a day late, but happy 40th birthday to Dungeons & Dragons, the animated series.

The first episode aired on September 17, 1983.

@MishaVanMollusq 😃

@hotdogsladies it is so good.

Unfortunately, Riemann was never in very good health, and in 1862 he developed tuberculosis. He convalesced in Italy off and on for a few years, but eventually succumbed to the illness, passing away in 1866. He was only 39 years old.

Riemann was supposedly working on something at the time, and there is an apocryphal story that many unpublished works –– the products of his "gloriously fertile originality" –– were carelessly discarded by someone cleaning out his quarters after he passed away.

It was Einstein, of course, who finally got it right. Riemann's work (following Gauss, Lobachevsky, and others) freed mathematicians from rigid notions of space and geometry, and provided Einstein with the mathematical framework needed to express the ideas of general relativity.

(That is, it was Einstein who first understood how Riemannian geometry applies in the physical world. He learned about the work of Riemann, Ricci, and others from his friend and colleague Marcel Grossman.)

Others would soon try to shape Riemann's ideas into a theory relating the motion of matter and the curvature of space.

W. K. Clifford's "Space Theory of Matter" (1876) is a notable example. He gets it precisely backwards compared to GR, emphasizing the importance of curvature at short distances rather than long ones. But the core idea — a dynamics for the geometry of space! — was truly remarkable.

Read it here: https://archive.org/details/proceedingscamb06socigoog/page/n176/mode/1up?view=theater

He also asked whether or not his approach to geometry, based as it was on mathematically local statements about space, could be a valid description of physical reality if matter is discrete.

Riemann suggested that this was a question for physicists, not mathematicians.

Riemann introduced a number of now-familar concepts in his lecture: the metric tensor as the quadratic form governing infinitesimal distances, curved spaces of arbitrary dimension, geodesics, normal coordinates, and the curvature tensor that now bears his name.

(Geometrically, the Riemann tensor tells you how a vector, or arrow, twists and turns if you try to keep it pointed in the same direction it was just pointing, while carrying it around a closed path on a curved surface.)

Riemann's approach is broader than the geometry axiomatized by Euclid.

He generalizes the infinitesimal version of the Pythagorean theorem describing the distance between two nearby points, and dispenses with the infamous 5th axiom.

(Euclid's 5th postulate says that if I give you a straight line and a point not on that line, both in a plane, you can draw a second line through the point that never intersects the first. That's not true on intrinsically curved surfaces like a globe or saddle.)

Riemann's lecture "On the Hypotheses Which Lie at the Foundations of Geometry," developing and expanding the ideas of his mentor Gauss into what we now call Riemannian geometry, was delivered in 1854.

A translation is available here:

http://lymcanada.org/wp-content/uploads/sites/2/2015/01/Riemann_Habilitation-Dissertation.pdf

Riemann was the star pupil of Gauss, who described Riemann's PhD thesis on complex variables as the work of someone with “a gloriously fertile originality.” Hold on to that phrase for your next rec letter!

A few years later, when Riemann was up for a faculty position, Gauss set him the task of reformulating the foundations of geometry.

No big deal, just the greatest mathematician of the age asking him to reformulate the foundations of a subject spelled out by Euclid some 2,000 years earlier.

Mathematician Bernhard Riemann was born #OTD in 1826.

He made deep contributions to complex analysis and number theory, but physicists remember him for his work on the foundations of geometry. These insights provide the mathematical framework for general relativity.

@aprilfollies I wondered the same! I didn’t see if it landed on it or with it. But it certainly seemed to be trying to get a response out of it!

@spiegelmama red tail, I think

Out in the suburbs last night, this handsome son of a gun landed right in front of my car.

It played with its dinner a bit, flipping it up in the air and pecking at it, lifting it with its talons and inspecting it from different angles. After a few minutes of this it flew over to a nearby fence.

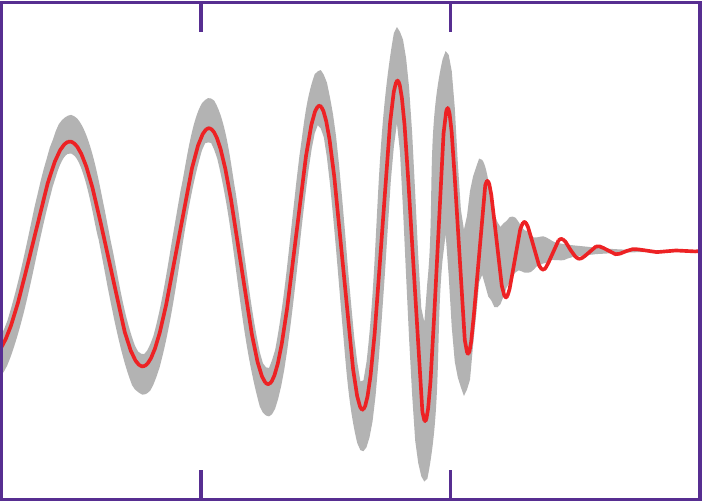
The latest signal, which landed earlier today, has a false-alarm rate of one per 35 years or so.

That's not ironclad, but it's pretty solid.

If it holds up, this was probably the result of a binary black hole merger like the initial detection on September 14, 2015.

https://gracedb.ligo.org/superevents/S230914ak/view/

LIGO / Virgo / KAGRA recently began the 4th observing run (“O4”) and signals are popping up fairly regularly.

You can keep an eye on the Public Alerts here:

https://gracedb.ligo.org/superevents/public/O4/

I mean, if that doesn't make you want to drop everything and marvel at the Universe, I don't know what will.