Conversation

Notices

1. Robert McNees (mcnees@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:37:58 UTC Robert McNees

   If there is one physics formula everyone knows, it's E = mc².

   Einstein proposed the famous equivalence between energy and mass in his second special relativity manuscript, which he submitted to Annalen der Physik #OTD in 1905.

   https://www.fourmilab.ch/etexts/einstein/E_mc2/www/

   • Robert McNees (mcnees@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:40:26 UTC Robert McNees

     in reply to

     As you may recall, yesterday was the 118th anniversary of the publication of Einstein's first special relativity paper in the journal.

     That paper lays out many of the results we associate with special relativity, except for the most famous one!

     The mass-energy equivalence result was submitted immediately after the first manuscript appeared in print.

     https://mastodon.social/@mcnees/111132114549253218

   • Robert McNees (mcnees@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:42:21 UTC Robert McNees

     in reply to

     Einstein jumps right in and picks up a thread from the first paper. He considers the energy of a massive object in two reference frames – one with the object is at rest, one where it moves at speed v – and considers a process where it emits energy.

     The image in the first post shows his conclusion: “If a body gives off the energy L in the form of radiation, its mass diminishes by L/V².” (In modern notation, E/c²). Einstein concludes that “The mass of a body is a measure of its energy-content.”

   • Robert McNees (mcnees@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:43:30 UTC Robert McNees

     in reply to

     Einstein wasn’t the first person to propose a relationship between changes in an object’s energy and inertia. A number of 19th century scientists suggested various relationships between a particle's mass and its energy content.

     But those proposals were poorly motivated, or imprecise, or both. And in most cases they applied only to certain sorts of mass or radiation.

   • Robert McNees (mcnees@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:44:20 UTC Robert McNees

     in reply to

     Einstein was the first to propose that the relationship goes beyond energy lost to particular types of radiation, and the first to arrive at the correct form of the equivalence.

     Most importantly, his arguments were based on a physical principle – relativity.

     So what can we get out of this equivalence?

   • Robert McNees (mcnees@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:45:33 UTC Robert McNees

     in reply to

     Some of the mass of unstable nuclei comes from binding energy, and fission in a reactor releases this as energy. Some of that energy can then be used to produce electricity.

     It's just a small fraction of the mass that gets converted, but that factor of c² is awfully big (c is 3 x 10⁸ m/s) so a little bit of mass goes a long way.

   • Robert McNees (mcnees@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:46:54 UTC Robert McNees

     in reply to

     There aren't really any practical methods for converting macroscopic amounts of mass entirely into energy. A particle and its anti-particle will annihilate and convert entirely into energy, but this makes it pretty hard to get your hands on a macroscopic amount of anti-particles.

     Imagine that, somehow, we could produce an anti-baseball. Just a regulation baseball, where every particle has been replaced by its associated anti-particle. What could we do with that?

   • Robert McNees (mcnees@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:48:07 UTC Robert McNees

     in reply to

     Well, a baseball has a mass of around 0.15 kg, give or take. According to special relativity, this is equivalent to an amount of energy

     0.15 kg * (3 x 10⁸ m/s)² = 1.35 x 10¹⁶ J.

     One Joule, "J", is the amount energy you'd expend lifting a 1kg mass about 10cm here on Earth.

     So you bring your baseball and your anti-baseball together and get twice that - a bit less than 3 x 10¹⁶ J.

     How much is that? A few years ago, in 2019, global energy consumption was about 600 exajoules, or 6 x 10²⁰ J.

   • John Francis (johnefrancis@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:48:58 UTC John Francis

     in reply to

     @mcnees love your threads. Maybe you want to followup on mass-energy equivalence with the emerging mass-energy-information equivalence?

   • Robert McNees (mcnees@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:49:10 UTC Robert McNees

     in reply to

     If we could extract all the energy from the mass of our baseball - anti-baseball pairs in a usable form, we'd need about 20,000 of them to cover what we, as a species, use in a year.

     This isn't possible, either. In nuclear fission only a fraction of the energy released is used to produce electricity. But let's not get hung up on details.

   • JD Long ✅ (cmastication@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:49:14 UTC JD Long ✅

     in reply to

     @mcnees <boooooom.gif>

   • Robert McNees (mcnees@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:49:31 UTC Robert McNees

     in reply to

     • John Francis

     @johnefrancis Thanks! I'll add it to the list.

   • John Francis (johnefrancis@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:50:02 UTC John Francis

     in reply to

     @mcnees you can do that, but it will make the list heavier!

   • Robert McNees (mcnees@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:52:01 UTC Robert McNees

     in reply to

     • LIGO

     Still, there are some examples of fantastically large masses being converted into an equivalent amount of energy! Just not in ways that we can harness.

     My favorite examples are the binary black hole mergers observed by @LIGO and the EGO Virgo collaborations.

     These mergers rapidly radiate so much energy in the form of gravitational waves that they are briefly more luminous than all the stars in our universe, combined.

   • Robert McNees (mcnees@mastodon.social)'s status on Wednesday, 27-Sep-2023 14:59:42 UTC Robert McNees

     in reply to

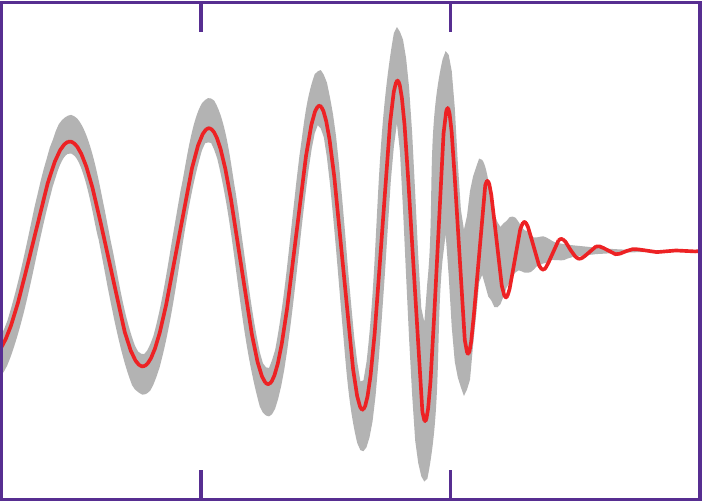
     During the GW150914 black hole merger, between 2.5 and 3.5 solar masses were converted to energy that was radiated as gravitational waves.

     One solar mass is about 2 x 10³⁰ kg, and the speed of light is 3 x 10⁸ m/s. So 3 solar masses is mc² = 1.8 x 10⁴⁷ J.

     Image: NASA

   • Robert McNees (mcnees@mastodon.social)'s status on Wednesday, 27-Sep-2023 15:00:34 UTC Robert McNees

     in reply to

     The rate at which the energy was radiated as gravitational waves was not uniform — there was a peak and then it fell off.

     But if we estimate most of it being radiated over the last 10ms or so of the merger, that’s a power output of around 2 x 10⁴⁹ Watts.

     That’s about 10 times the luminosity of all the visible stars and galaxies in our universe!

   • Robert McNees (mcnees@mastodon.social)'s status on Wednesday, 27-Sep-2023 15:02:59 UTC Robert McNees

     in reply to

     Anyway, of all the important results Einstein published in his "miracle year" of 1905, the astounding and unexpected equivalence between mass and energy is the one that lodged itself in the popular consciousness.

     Happy E = mc² day!

   • John Francis (johnefrancis@mastodon.social)'s status on Wednesday, 27-Sep-2023 16:07:48 UTC John Francis

     in reply to

     @mcnees wow, that's a lot of power. I wonder how much of it ends up converted back to mass as it radiates away and crashes into other...mass.